delta of an at-the-money binary option

Classic Options

The Classic Options Pricer allows the user to toll and analyze the greeks of three products: European, American and Digital Options (Calls and Puts).

European Options

European Options and the behavior of their Greeks accept already been largely discussed in chapter 4 and chapter 5 respectively.

The Classic Options Pricer offers a perfect opportunity to put all this theory into practice.

American Options

American options can exist exercised at whatsoever fourth dimension during their life. Since investors have the freedom to exercise their American options at any point during the life of the contract, they are logically more than valuable than European options.

The Archetype Options Pricer prices American Options using the approximation method of Bjerksund and Stensland (1993).

American Calls

For American Calls, early exercise may exist optimal simply before the dividend payment if the dividend payment is large enough.

This can be expressed by the following condition: \(\frac{D}{K} > r * (T-t)\).

Intuitively, if one exercises the American call, he pays a specific amount of money to buy the underlying shares. On the one hand, he doesn't receive interest on this greenbacks amount; and, on the other, he would receive time to come dividends for property the stocks. In other words, if the dividend yield is higher than the interest rate until maturity, it is optimal to practice the American telephone call. For stocks non paying dividends, it is never optimal to exercise the American call.

American Puts

Ultimately, it tin can exist optimal for the holder of an American put option to choose to exercise if the interest rate that would exist received on a cash deposit equal to K is college than the dividend payments until maturity. For non-dividend-paying stocks, an American put should always be exercised when it is sufficiently deep ITM.

It is important to realize that it makes no sense to exercice an option when there is time premium remaining because you are throwing away that time premium past doing so. Yous would be improve of selling the option than exercising information technology.

Digital Options

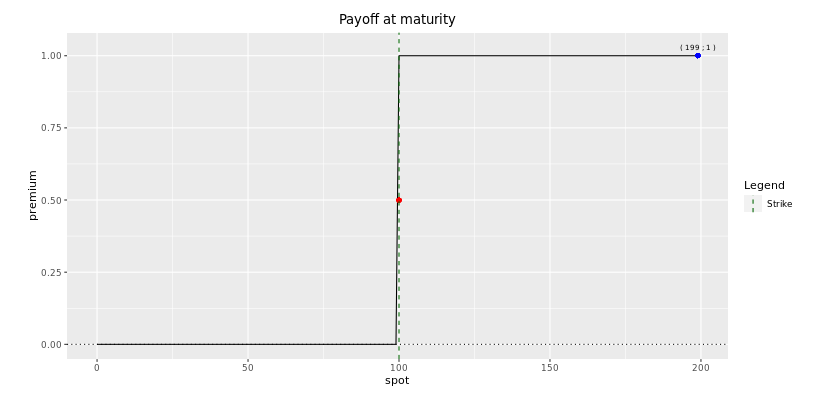
Digital options are quite straigthforward. They are options that pay a fixed coupon if the underlying is below or to a higher place a predetermined level and does non give a payout at all in all other cases.

Digitals are yet considered as exotic options as they cannot be perfectly replicated past a set of standard options.

European Digitals

We will focus on Digital Calls but the aforementioned reasoning can always be applied in the example of Digital Puts.

Payoff and Premium

European Digital Calls pay a fixed coupon C if the underlying spot toll at maturity T is higher than a predetermined barrier level, K.

The Digital Telephone call payoff can be expressed as: C * \(1_{\{S_T > H\}}\). This is why we too telephone call them binary Calls.

Nether Black–Scholes, the cost of such an option is given by the following formula:

\(\boxed{\text{Digital Telephone call} = C * N(d_2) * e^{-rT}}\)

So the Digital Call price is given by \(N(d_2)\), which is nothing simply the negative of the derivative with respect to K. Information technology gives the probability that the spot at time T is higher than the bulwark level.

This shape should exist familiar to yous by now. It looks like the Delta of a European Telephone call. This is due to the fact that this Delta is given by \(N(d_1)\), which is besides a cumulative distribution function.

If the shape of the premium looks like the shape of the delta of European call, then the delta of a digital call will be the gamma of a vanilla telephone call. As we will see, this means that we no longer have this bounded delta from zero to 1.

Equally you volition see, Digital Calls are used extremely often in the world of structured products equally their payoffs generally contain some sort of discontinuity.

Replication of European Digital Options

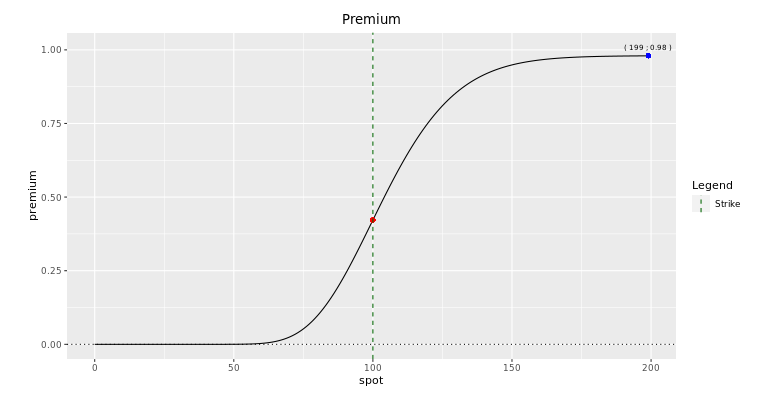
The digital call can be thought of as a limit of a call spread. One can therefore brand a good judge of the toll of a digital selection by using option spreads.

Digital (K) = \(\text{lim}_{\epsilon \rightarrow 0} \; \frac{i}{2 \epsilon} \left( Call(G-\epsilon) - Call(One thousand+\epsilon)\right) = - \frac{\partial Call(K)}{\fractional K}\)

As the distance between the call pick strikes and the digital strikes, \(\epsilon\), gets smaller, nosotros demand \(\frac{one}{\epsilon}\) call spreads of width \(2\epsilon\) to replicate the digital. In the limit, meaning every bit \(\epsilon\) approaches nil, the call spread replicates the digital exactly.

Notation that the to a higher place expression is theoretical every bit, in practice, a trader will not center the call spread around the barrier. He will exist more defensive and accept a telephone call spread that over-replicates the digital as shown beneath.

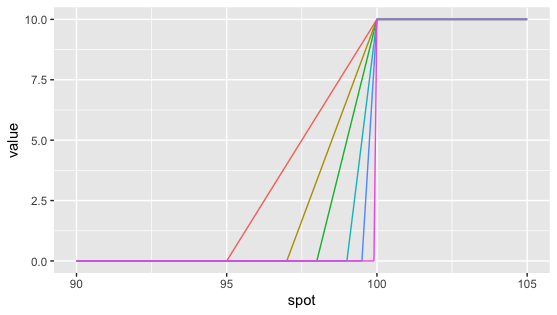
Hedging a Digital

Well, you should not be surprised if I tell you that the simply existent way to take chances manage the digital option is with option spreads.

You can then hedge a digital call equally a call spread. The gearing of the call spread used to over-replicate the digital depends on the strike width of the call spread. The wider the telephone call spread, the lesser the gearing and the more conservative the price.

What practice nosotros mean by saying that the call spread over-replicates the digital option?

Let u.s.a. accept a await at Fig 6.3. here above.

To a higher place the bulwark level, the call spread has the same payoff as the digital call. Beneath the barrier level, the digital telephone call has a zip payoff merely the call spread has a non-cypher payoff between its lower strike and its upper strike located at the barrier level. Therefore, we say that the call spread over-replicates the digital call considering its payoff (and therefore its premium) is e'er greater or equal to the digital telephone call's payoff.

Allow us take a small practical example.

As an investor, y'all buy a 6-month European digitall call on AB Inbev which pays 10€ if after 6 months the ABI stock trades above 50€ and pays 0 if the ABI stock trades beneath 50€ at maturity.

Every bit a trader, I sell you this digital call on ABI stock. How much will I sell information technology to y'all? Well, I will replicate the digital using a geared phone call spread. I believe that a 2€ wide call spread should exist plenty for me to risk manage this position. So I will cost the digital call as if it was a 48€/50€ telephone call spread that is 5 times geared.

Y'all tin think of unlike scenarii and see that this telephone call spread over-replicates the digital call.

By doing and then, I have therefore priced the digital conservatively. I could accept been more than aggressive past choosing a tighter 49€/l€ call spread. But remember that I accept risks to manage, especially gamma and pin risk around the 50€ bulwark level.

The smaller the phone call spread, the more aggressive the price merely the more than difficult the hedging.

For a digital option, Gamma can exist quite big and tricky near the bulwark at maturity. Recollect about the state of affairs where you are just before expiry, the ABI stock trades at fifty€ so that the digital would not pay you anything. If ABI stock goes up to 50.02, the digital would suddenly pay you 10€. As a trader, this would exist extremely difficult to hedge. Equally a trader, the telephone call spread gives me a cushion against this risk.

Using a call spread allows to shine the Greeks. The smaller the phone call spread, the larger Gamma and Vega can go almost the barrier. In fact, around the barrier level, they shoot upwardly and then shoot downward while changing sign.

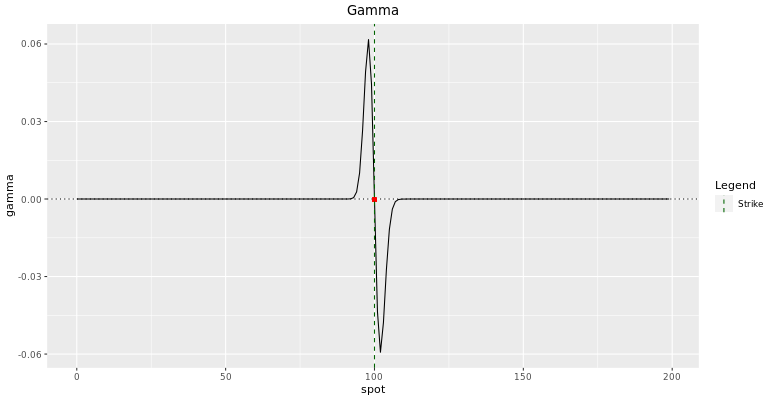
We will analyze Call Spreads in more details in the side by side chapter. You lot will see that its gamma is smoother than that of a digital call. The larger the strike width, the more this is true.

Y'all shoud have understood by at present that when I sell a digital call, I actually volume and trade a call spread in my run a risk direction system. As the underlying gets closer to the barrier, you still desire to be able to manage your delta hedge properly. A big Gamma means that you will accept to purchase/sell a large Delta of the underlying, which might be difficult in the market. It is the reason why the liquidity of the underlying is an important variable when selecting the strike width of the replicating call spread.

Width of the Call Spread and Bulwark Shifts

And then the width of the selection spread is used as a pricing machinery to become bourgeois on the price of a digital option over its model price.

It is necessary in the pricing machinery to account for real-world difficulty in executing large deltas at the barrier that the model does not consider.

The optimal width of the phone call spread depends on several parameters among which the size of the digital, the size of the nominal, the underlying's liquidity, the peak delta around the bulwark and the implied volatility around the bulwark.

In practise, some traders rather take a constant shift of the bulwark. Basically, it allows them to take an additional margin for managing the risks if the underlying was to get close to the barrier. This tin exist more efficient when risk managing a large volume of exotic options.

When taking a bulwark shift, a trader is pricing a new digital whose replicating centered call spread is the hedge of the actual digital.

The direction of the barrier shift manifestly depends on the trader's position.

We will discuss further almost barrier shifts in the chapter on barrier options.

Adventure Analysis - The Greeks

Nosotros will shortly speak about the greeks of a digital call at initiation. Note that the risks and therefore the greeks are dynamics. For instance, the greeks will be quite different if y'all get closer to maturity. As I cannot describe every scenario, the best mode for you to learn this fabric is to utilize the pricer, ask yourself many questions and find your answer using the pricer. For example, what happens to the greeks if just earlier maturity the spot price is exactly at the barrier level? You open the pricer, you select Digital phone call in the option type input, y'all set the stock price at the strike level and you lot set the maturity close to 0. You volition be able to calculate the greeks and see all the related graphics. You will then have to interpret them. If you have any questions, you can always drib us an email at info$@$derivativesacademy.com

Delta

The holder of a digital phone call is always long the forward price since a higher frontwards increases the probability of the option finishing in-the-money.

Being long the forrard means being: - Long involvement rate - Short dividends - Short infringe costs

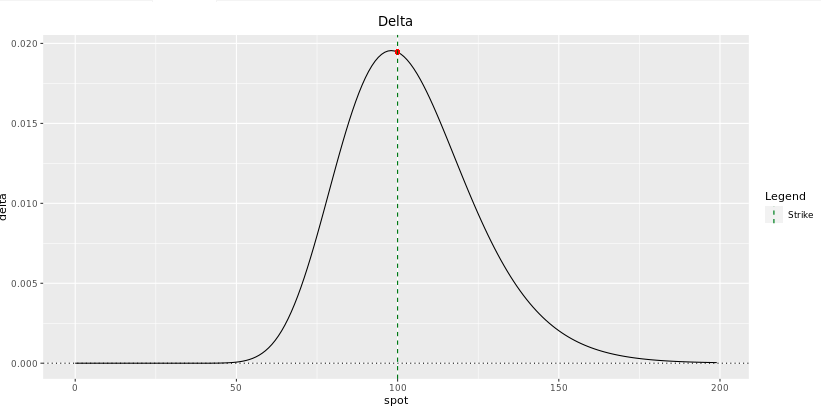
Fig: 7.5 :Delta of a i-year Digital Phone call at initiation

I don't retrieve I am making yous a favor if I describe all the graphics with precision. The all-time fashion to develop yourself is to decipher these plots past yourself. For instance, yous should be able to understand why does the delta converges to nil (and not to 1 as in the instance of European calls) when the stock price increases well above the bulwark level. Note that the plot of the delta is simply the first derivative of the premium plot with respect to the spot price.

Since a digital phone call has positive delta, the trader selling it will have to buy delta of the underlying. Therefore the trader will be long dividends, short interest rates and long infringe costs of the underlying.

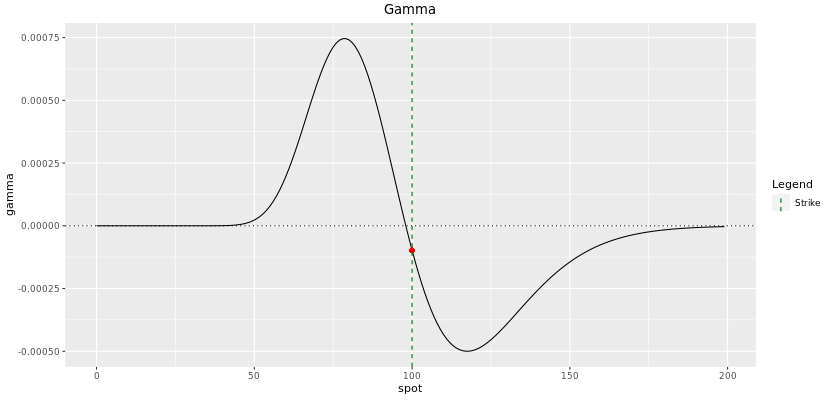
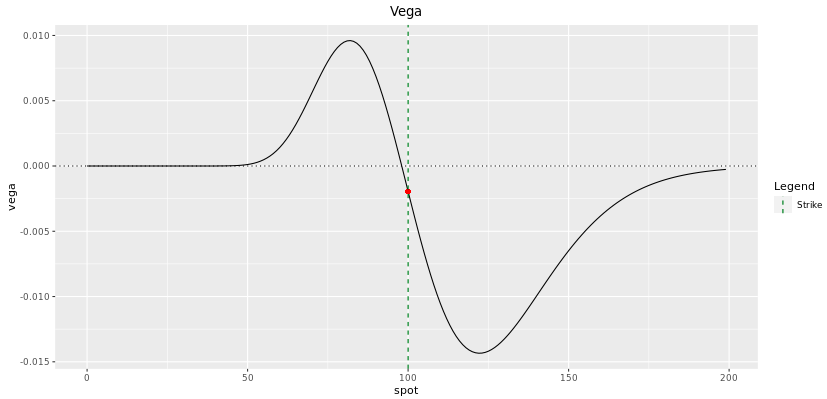
Gamma

While their magnitudes are quite dissimilar, Gamma and Vega carry similarly and depend almost the position of the frontward price regarding the barrier. The Gamma plot can be hands deduced from the Delta plot since it is simply the kickoff derivative with respect to the spot price. Dissimilar vanilla options, the gamma of digital options change sign effectually the barrier level. While this change is quite shine at initiation, we take seen that it gets more spiky closer to maturity. It makes the hedging procedure particularly difficult for the trader as vega and gamma shoot upwardly and down while irresolute sign.

Retrieve about being the trader hedging this digital phone call shut to maturity when the spot is around the bulwark level. How does this alter of sign impact your delta hedging?

This aperture risk (gap risk) has been discussed and is the reason why barrier shifts are applied and selection spreads are used to smooth it.

Vega

The fact that vega depends on the position of the forward toll with respect to the barrier is very intuitive.

The holder of a digital call will be long volatility if the frontward cost is lower than the bulwark level since a higher volatility will increase the probability of the spot finishing to a higher place the barrier at maturity. When the forrad is lower than the barrier, yous can think of the digital call as being out-of-the money. Volatility volition increase the probability of the option going from OTM to ITM.

Inversely, the holder of a digital phone call volition be short volatility if the forward price is greater than the barrier level since a higher volatility will subtract the probability of the spot finishing above the barrier at maturity. When the forward is greater than the barrier, you can call back of the digital telephone call as being in-the money. Volatility volition increase the probability of the option going from ITM to OTM.

Theta

The shape of Theta plot looks completely opposite to the shape of Vega plot. This is because time to maturity has a similar result to a digital pick price every bit volatility. The effect is not exactly the same as time has always a 2d effect that comes from the discounting affect, altough this last event is more often than not less important.

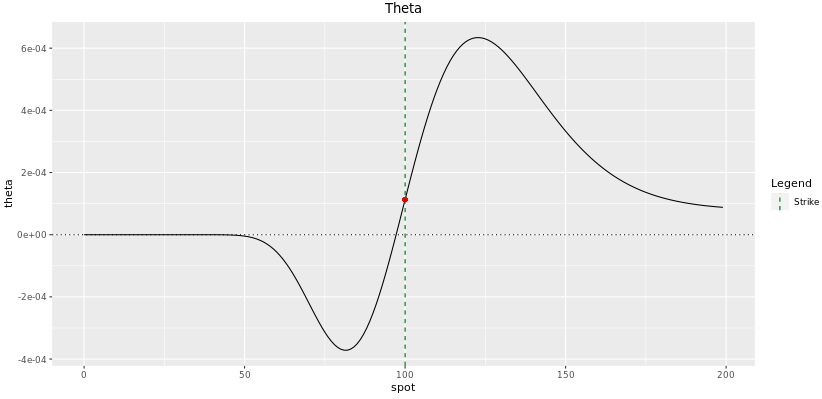
Fig: 7.eight : Theta of a 1-twelvemonth Digital Call at initiation

Rho

When we spoke about Rho in section 5.6.1, we said that the event of interest rate on an option'southward price came from two effects: the cost of delta-hedging and the discounting.

It is therefore non very surprising to see similarities between the Delta profile and the Rho contour. Note that the discounting effect is clearly apparent in the right-side of the curve where the option is completely in-the-money and at that place is no delta left. On that side of the curve, Rho is negative because an increase in interest rates inscreases the disbelieve factor and therefore decreases the nowadays value of the digital call. How much the Rho is negative will and so mainly depend on the fourth dimension to maturity.

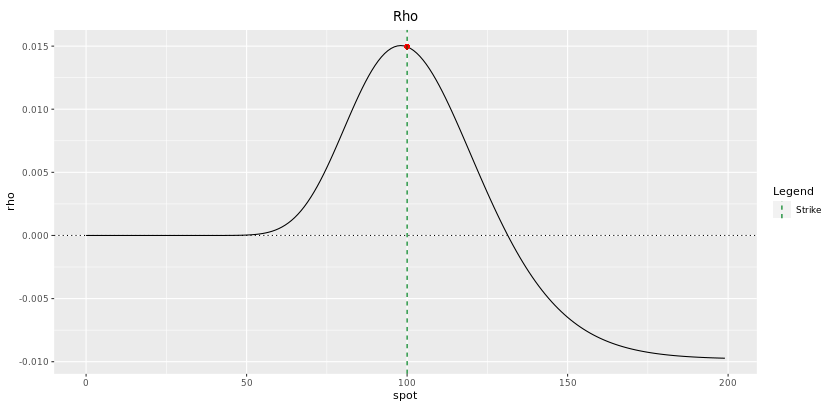
Fig: seven.9 : Rho of a one-year Digital Telephone call at initiation

Skew

Since a trader hedges a digital option using an selection spread, the skew risk is a critical consideration.

Let united states assume that we just sold a digital call, we will hedge it by buying a call spread. Taking a long position in a call spread means ownership a phone call at a lower strike and selling a call at an upper strike. The skew makes the lower strike unsaid volatility more than expensive than the upper strike unsaid volatility. Since the skew makes the hedge more expensive, it makes the construction itself more expensive. Call up what nosotros said in section 4.v, an option price is nada else but the cost of the hedge!

Therefore the skew makes the cost of digitals more expensive. - A long position in a digital telephone call is long the skew. - A short position in a digital call is short the skew.

Since digital options are sensitive to skew, you must apply a model that knows near skew. When pricing European digitals, then your calibration should focus on getting the skew at maturity correct. When pricing American digitals with path-dependency, you will demand to use some smooth surface calibration to capture the effect of surface through time. In other words, when dealing with these path-dependent american digitals, yous are non but sensitive to the volatility at maturity but to many volatilities before maturity. Your volatility hedge will and then consist of several European options with different maturities. We speak about vega buckets. The book of Adil Reghai is particularly good to grasp the concept of vega buckets and vega KT.

American Digitals

For American digitals, the trigger condition tin can be activated at anytime before maturity.

There exists a fantastic approximate link between European digital options and American digital options.

I felt quite stupid while learning virtually information technology as it is actually quite intuitive :). Dorsum in 2015, I used to effort estimating the cost of every exotic pick before pricing them. I was trying to develop every bit much every bit possible my intuition in terms of pricing and sensitivities in every market place scenario. I quickly realised that the price of American digitals were e'er approximately twice the price of European digitals (with the same characteristics obviously!). The price of European digitals beingness quite easy to estimate, the approximations for American digitals were not also bad. One solar day, I decided to stay a bit afterward the floor and start plotting Monte Carlo simulations to compare the price sensitivity of a bulwark selection to the barrier level with respect to the underlying'due south forward. Doing so, I realised why the in a higher place human relationship between American and European digitals were so consistent. This is simply the consequence of a well-known principle followed by brownian motion: the reflection principle.

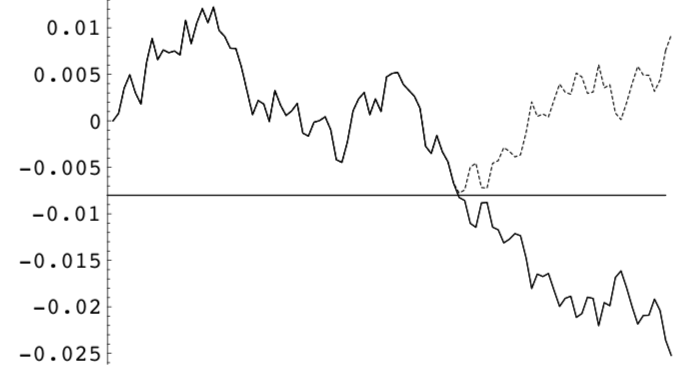
The Reflection Principle

In the theory of probability for stochastic processes, the reflection principle for a Wiener process states that if the path of a Wiener process W(t) reaches a value W(s) = a at fourth dimension t = southward, then the subsequent path after fourth dimension s has the same distribution equally the reflection of the subsequent path about the value a In other words, if W(southward) = a so Due west(t) is just as likely to exist above the level a every bit to be below the level a for s < t.

By assuming in our models that the log-returns of the underlying are normally distributed with null log-drift (with hateful zero), the normal distribution introduces the symmetry of the reflection principle.

Gatheral expresses it nicely in his lecture on Barrier options. In Fig 6.5 below, the dashed path has the aforementioned probability of being realized as the original solid path. We deduce that the probability of hitting the barrier B is twice the probability of ending up below the barrier at expiration. Putting this another style, the value of an American digital option is twice the value of a European digital selection. Note that this relationship won't exist exactly respected when the log-drift is not zip (understand when the forward level is unlike from the spot level).

No-Bear upon Options

No-touch on digital options pays a coupon if the barrier has never been touched during the option life.

It seems clear that the event of never touching the bulwark is complementary to the issue of ever touching it. Therefore, the probability of never touching the bulwark is nothing else but one minus the probability of ever touching the bulwark. From this parity, we tin easily deduce the price of a no-touch digital option knowing the price of the american digital pick and vice versa.

Source: https://bookdown.org/maxime_debellefroid/MyBook/classic-options.html

Posted by: bojorquezstentartudge.blogspot.com

Share this post